【机经解析】20181223库（数学）1223-0102

1. 质数问题

定义：在大于1的自然数中，除了1和它本身以外不再有其它因数。

特点：2是最小的、且唯一一个偶数性质的质数

本次题库出现的题目：

A=-1，n 是前 404 个质数的和，求 ~$A+A^n+A^{n+1}+A^{n+2}$~

思路：

前404个质数中，除了2，其它都是奇数，

因为：偶+奇=奇，奇+奇=偶

所以：n是奇数，n+1是偶数，n+2是奇数

~$A+A^n+A^{n+1}+A^{n+2} = -1+ (-1)+1+(-1) = -2$~

2. 分解质因数问题

定义：把一个合数分解成若干个质因数的乘积的形式

方法：合数从最小的质数开始除（2,3,5…），直到结果为质数为止

本次题库出现的题目：

求x和y

条件1：~$3^x$~×~$5^y$~=1125， 

条件2：y=3

思路：

1125 = 3×3×5×5×5 = ~$3^2$~×~$5^3$~

3. 圆心角与圆周角问题

圆心角等于同一弧所对的圆周角的二倍

本次题库出现的题目：

如图，∠AOB =130°，∠AEB=50°，求∠EAC

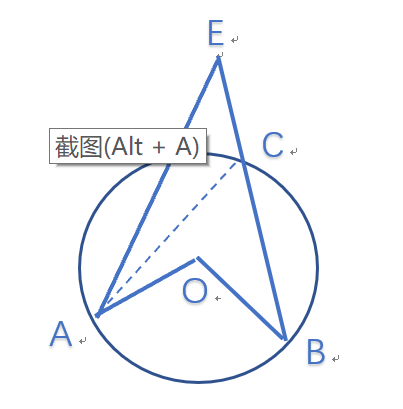
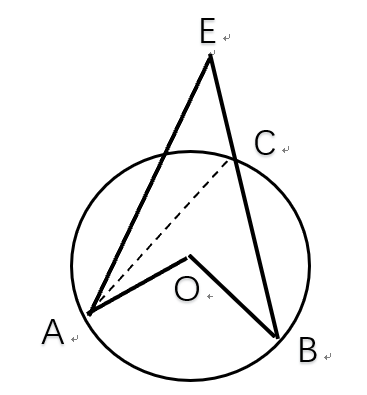
思路：

根据“圆心角是同弧圆周角的二倍”可得，∠ACB=65°，

∠EAC=180°-∠AEC-∠ACE =180°- 50°- (180°- 65°) = 15°