《毕出21套》解析：数学第1套

数学第1套PS

1.How many positive integers n have the property that both 3n and n/3 are 4-digit integers?

(A) 111

(B) 112

(D) 334

(E) 1,134

解：

要想保证3n和n/3都是4位数，则n最大为3333，最小为3000。

在【3000, 3333】中能够被3整除的数有3000，3003，3006，3009，……，3333。从3001开始，每3个数必然出现一个能被3整除的数，共有333/3 = 111个，加上3000自己，共有112个。答案为B。

2.If Whitmey wrote the decimal representations for the first 300 positive integer multiples of 5 and did not write any other numbers, how many times would she have written the digit 5?

(A) 150

(B) 185

(D) 200

(E) 201

解：

题目的意思是：在十进制下，写出前300个5的倍数的正整数，问5写了多少次。

这里前300个，相当于是公差为5的等差数列的前300项。5-1500，刚好三百个。

那么千位是不可能写5了，考虑个位，十位和百位分别会出现多少次5

个位是5，前三位从000-149 （个位是5，不可能是150，超过1500了）都可以，所以是150次

十位是5，个位只有5和0两种，前两位 00-14, 所以是15*2=30次

百位是5，个位只有5和0两种，十位是0-9，千位是0的时候，有20次，千位是1，只有1500，一次

一共150+30+20+1=201。答案为E。

3.If x < y < z and y - x > 5, where x is an even integer and y and z are odd integers, what is the least possible value of z-x?

(A) 6

(B) 7

(D) 9

(E) 10

解：

问题问的z -x最小，核心是求z最小。

由y-x>5可得出y>x+5，因为x是偶数，偶数+奇数为奇数，所以y的最小值为x+5+2（不能+1，因为奇数+奇数是偶数，不满足y是奇数的题设）。

zy都是奇数，所以z最小为y+2，即，x+7+2。由此可知，z-x最小为9，答案为D。

4.If the product of the integers w, x, y, and z is 770, and if 1 < w < x < y < z, what is the value of w + z?

(A) 10

(B) 13

(D) 18

(E) 21

解：

对770做质因子分解，即，2*5*7*11。可得w = 2；z =11。答案为B。

5.An "Armstrong number" is an n-digit number that is equal to the sum of the nth powers of its individual digits. For example, 153 is an Armstrong number because it has 3 digits and 13+53+33=153. What is the digit k in the Armstrong number 1,6, k, 4？

(A) 2

(B) 3

(D) 5

(E) 6

解：

要明白，这里是1是千位，6是百位，k是十位，4是个位。要想满足Armstrong number，则有：

14+64+k4+44=1604+10*k （这里最关键的就是把16k4变成1604+10*k ）

k(k3-10) = 1604-1553=51

则有：k=3，答案为B。

6.If n=p2 and p is a prime number greater than 5, what is the units digit of n2?

(A) 1

(B) 3

(D) 7

(E) 9

解：

这种题不需要搞清楚原理。只需随意带入一个满足条件的数即可。例如，p = 7。由此可知，n2为四个7相乘，个位数为1，答案为A。

7.Let S be the set of all positive integers having at most 4 digits and such that each of the digits is 0 or 1. What is the greatest prime factor of the sum of all the numbers in S?

(A) 11

(B) 19

(D) 59

(E) 101

解：

本题的难点在于如何准确不漏地找到所有符合要求的数。只能从小到大枚举，满足条件的有：

0，1，10，11，1000，1001，1010，1011，1100，1101，1110，1111

它们的和为8888 = 2*2*2*11*101。最大的质因子为101，答案为E。

8.When the integer n is divided by 17, the quotient is x and the remainder is 5. When n is divided by 23, the quotient is y and the remainder is 14. Which of the following is true?

(A) 23x+17y=19

(B) 17x-23y=9

(D) 14x+5y=6

(E) 5x-14y=-6

解：

依题意可写出：

n = 17x + 5 = 23y + 14，由此可解出17x-23y=9，答案为B。

9. 1,234

1,243

1,324

........

+4,321

The addition problem above shows four of the 24 different integers that can be formed by using each of the digits 1, 2, 3, and 4 exactly once in each integer. What is the sum of these 24 integers?

(A) 24,000

(B) 26,664

(D) 60,000

(E) 66,660

解：

这24个数中千位、百位、十位、个位的和都是60

60*(103 + 102 + 10 + 1) = 66660，答案为E。

10.A computer can perform 1,000,000 calculations per second. At this rate, how many hours will it take this computer to perform the 3.6 x 1011 calculations required to solve a certain problems?

(A) 60

(B) 100

(D) 1,000

(E) 6,000

解：

简单的除法，不要把单位算错即可，最后问题问的是多少小时，一小时有3600秒。答案为B。

11.A school supply store sells only one kind of desk and one kind of chair, at a uniform cost per desk or per chair. If the total cost of 3 desks and 1 chair is twice that of 1 desk and 3 chairs, then the total cost of 4 desks and 1 chair is how many times that of 1 desk and 4 chairs?

(A) 5

(B) 3

(D) 5/2

(E) 7/3

解：

本题比较简单。设desk的价格为d，chair的价格为c，依题意可得：

3d+c=2d+6c

d=5c

因此，4张书桌和1张椅子的价格为21c；1张书桌和4张椅子的价格为9c，两者的比值为7:3，答案为E。

12.

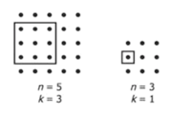
Let n and k be positive integers with k ≤ n. From an n × n array of dots, a k × k array of dots is selected. The figure above shows two examples where the selected k × k array is enclosed in a square. How many pairs (n, k) are possible so that exactly 48 of the dots in the n × n array are NOT in the selected k × k array?

(A) 1

(B) 2

(D) 4

(E) 5

解：

要先看懂题目，本题问的是，有多少组(n, k)能保证n × n这个矩阵减去k × k这个矩阵刚好是48个点。由此可得：

n*n - k*k = 48

(n - k) * (n + k) = 48

将48做质因子分解可得48 = 24*3。可以有4组两数相乘的情况：

(2，24), (4，12), (8，6), (16，3)

小的数=n-k，大的数=n+k，因为n-k+n+k=2n, n是整数，所以两数的和只能是偶数, 去掉(16，3) 的组合，剩下3组，答案为C。

13.A car traveled 462 miles per tankful of gasoline on the highway and 336 miles per tankful of gasoline in the city. If the car traveled 6 fewer miles per gallon in the city than on the highway, how many miles per gallon did the car travel in the city?

(A) 14

(B) 16

(D) 22

(E) 27

解：

设每箱有n加仑。462/n-336/n=6, 解得n=21

每加仑的公里数=每箱的公里数/每箱的加仑数=336/21=16，答案为B。

14.

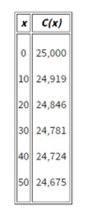
A certain manufacturer uses the function C(x)=0.04x2-8.5x+25,000 to calculate the cost, in dollars, of producing x thousand units of its product. The table above gives values of this cost function for values of x between 0 and 50 in increments of 10. For which of the following intervals is the average rate of decrease in cost less than the average rate of decrease in cost for each of the other intervals?

(A) From x=0 to x=10

(B) From x=10 to x=20

(D) From x=30 to x=40

(E) From x=40 to x=50

解：

函数C(x)是一元二次函数，由于0.04>0，所以该抛物线开口向上。对称轴为-b/2a = 106.25。也就是说，在小于106.25的范围内，越靠近106.25，该抛物线的斜率越小，也就是下降率越低，显然选项E更靠近106.25，答案为E。

15.There were 36, 000 hardback copies of a certain novel sold before the paperback version was issued. From the time the first paperback copy was sold until the last copy of the novel was sold, 9 times as many paperback copies as hardback copies were sold. If a total of 441,000 copies of the novel were sold in all, how many paperback copies were sold?

(A) 45,000

(B) 360,000

(D) 392,000

(E) 396,900

解：

题干翻译：在发行平装本之前，已售出36，000本小说的精装本。从第一本平装本销售到小说最后一本销售，平装本的销量是精装本的9倍。

这里是在说，在销售期间的平装是精装的9倍。不要想复杂（因为这两个条件是逗号隔开的），不要考虑那36000的影响。

设hardback为X，paperback为Y

X + Y = 441000 - 36000 = 405000

9X = Y

Y = 364500，答案为C。

16.A certain truck traveling at 55 miles per hour gets 4.5 miles per gallon of diesel fuel consumed. Traveling at 60 miles per hour, the truck gets only 3.5 miles per gallon. On a 500-mile trip, if the truck used a total of 120 gallons of diesel fuel and traveled part of the trip at 55 miles per hour and the rest at 60 miles per hour, how many miles did it travel at 55 miles per hour?

(A) 140

(B) 200

(D) 300

(E) 360

解：

设题目所求为X

X/4.5 + (500 - X)/3.5 = 120

这个方程解起来比较麻烦，我们可以直接带入五个选项试，答案为E。

17.A merchant paid $300 for a shipment of x identical calculators. The merchant used two of the calculators as demonstrators and sold each of the others for $5 more than the average(arithmetic mean) cost of the x calculators. If the total revenue from the sale of the calculators was $120 more than the cost of the shipment, how many calculators were in the shipment?

(A) 24

(B) 25

(D) 28

(E) 30

解：

本题要先理解shipment的意思，这里不是运费，而是整个的费用。设在这批货中的calculators数量为x，则有：

(300/x + 5)(x-2) = 420

解得x = 30，答案为E。

18.If there is a least integer that satisfies the inequality 9/x ≥2, what is that least integer?

(A) 0

(B) 1

(D) 5

(E) There is not a least integer that satisfies the inequality

解：

本题问的是满足题干条件中的x的最小值。显然x是负数时不满足条件，0不能做分母，答案只能为1，即，选项B。

19.The sum of the ages of Doris and Fred is y years. If Doris is 12 years older than Fred, how many years old will Fred be y years from now, in terms of y?

(A) y-6

(B) 2y-6

(D) 3y/2-6

(E) 5y/2-6

解：

本题还是要先将题目看懂。题干中的how many years old will Fred be y years from now翻译过来是“y年后， F多大”。

设D和F分为两人的年龄

D + F = y

D - F = 12

F = y/2 - 6

题目y 年之后F的年龄多大

F + y =3y/2 – 6，答案为D。

20.If k≠0 and k- (3−2k2)/k = x/k, then x=

(A) -3-k2

(B) k2-3

(D) k-3-2k2

(E) k-3+2k2

解：

本题非常简单，等式两边同乘以k即可，注意最开头的k，答案为C。

21.King School has an enrollment of 900 students. The school day consists of 6 class periods during which each class is taught by one teacher. There are 30 students per class. Each teacher teaches a class during 5 of the 6 class periods and has one class period free. No students have a free class period. How many teachers does the school have?

(A) 25

(B) 30

(D) 60

(E) 150

解：

900个学生，6个课时，1个老师教1个班，每个班30个学生，每个老师教5个课时休息1个课时。

900/30=30个班

30*6=180课时

180/5=36个老师，答案为C。

22.Each of the integers from 0 to 9, inclusive, is written on a separate slip of blank paper and the ten slips are dropped into a hat. If the slips are then drawn one at a time without replacement, how many must be drawn to ensure that the numbers on two of the slips drawn will have a sum of 10？

(A) Three

(B) Four

(D) Six

(E) Seven

解：

本题要求保证一定有两数相加为10。共有情况如下：

1+9

2+8

3+7

4+6

极端情况下（前六张取了0，1，2，3，4，5），要取7个才能确保有两张纸的数字和为10。

23.

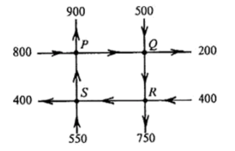
The figure above represents a network of one-way streets. The arrows indicate the direction of traffic flow and the numbers indicate the amount of traffic flow into or out of each of the four intersections during a certain hour. During that hour, what was the amount of traffic flow along the street from R to S if the total amount of traffic flow into P was 1, 200?

(Assume that none of the traffic originates or terminates in the network)

(A) 200

(B) 250

(D) 350

(E) 400

解：

本题看起来很乱，但其实很简单。

P是1200，流入P点的是800和S，流入S的是550和R，但是S还要流出400。

1200-800+400（加回S流出的400）-550（减去流入的550）=250（PS），答案为B。

24.Machines X and Y run at different constant rates, and machine X can complete a certain job in 9 hours. Machine X worked on the job alone for the first 3 hours and the two machine working together, then completed the job in 4 more hours. How many hours would it have taken machine Y, working alone, to complete the entire job?

(A) 18

(B) 13+1/2

(D) 4+1/2

(E) 3+2/3

解：

设那项工作为1，Y需要T小时独自完成那项工作

X的速率为 1/9，Y的速率为 1/T

7*1/9 + 4*1/T = 1

解得：T = 18，答案为A。

25. When a certain stretch of highway was rebuilt and straightened, the distance along stretch was decreased by 20 percent and the speed limit was increased by 25 percent. By what percent was the driving time along this stretch reduced for a person who always drives at the speed limit?

(A) 16%

(B) 36%

(D) 45%

(E) 50.25%

解：

设原长度为D，原限速为S。依题意，现在的长度和限速分别为0.8D和1.25S。总时间为过去的0.8/1.25 = 0.64，即，比原来减少了36%，答案为B。

26.The annual stockholders' report for Corporation X stated that profits were up 10 percent over the previous year, although profits as a percent of sales were down 10 percent. Total sales for that year were approximately what percent of sales for the previous year?

(A) 78%

(B) 90%

(D) 122%

(E) 190%

解：

1.1*P1/ S2 = 0.9*P1/S1

S2= 1.1*S1/0.9= 1.222*S1，答案为D。

27.A certain brand of house paint must be purchased either in quarts at $12 each or in gallons at $18 each. A painter needs a 3-gallon mixture of the paint consisting of 3 parts blue and 2 parts white. What is the least amount of money needed to purchase sufficient quantities of the two colors to make the mixture?

(4 quarts= 1 gallon)

(A) $54

(B) $60

(D) $90

(E) $144

解：

依题意：题目要求有3加仑的混合物，所以核算下来蓝色需要1.8加仑，白色需要1.2加仑。

蓝色：1.8加仑=7.2夸脱

白色：1.2加仑=4.8夸脱

每一夸脱12，每一加仑18。

蓝色都用加仑买为36。用加仑搭配夸脱买为（1加仑+4夸脱）66，显然都用加仑划算。

白色都用加仑买为36，用加仑搭配夸脱买为（1加仑+1夸脱）30，显然搭配更划算。

答案为66，选C。

28.

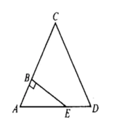
If each side of △ACD above has length 3 and if AB has length 1, what is the area of region BCDE?

(A) 9/4

(B) (7/4)√3

(D) (7/2)√3

(E) 6+ √2

解：

三角形ACD为等边三角形，角A是60度。由此可知AE长度为2，BE长度为√3。三角形ABE的面积为√3/2。三角形ACD的面积为(9/4) √3。四边形BCDE的面积为两个三角形面积相减，答案为(9/4) √3 - √3/2 = (7/4)√3，答案为B。

29.

The figure above shows some of the dimensions of a triangular plaza with an L-shaped walk along two of its edges. If the width of the walk is 4 feet and the total area of the plaza and walk together is 10,800 square feet, what is the value of x?

(A) 200

(B) 204

(D) 216

(E) 225

解：

本题需要做一条辅助线：

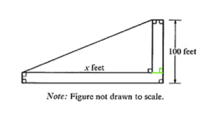
依题意，绿线长度为4。则整个L型过道被分为了横和竖两部分。横部分的面积为4*(x+4)；竖部分面积为：96*4。带入总面积为10800，求得x = 200，答案为A。

30. The surface distance between 2 points on the surface of a cube is the length of the shortest path on the surface of the cube that joins the 2 points. If a cube has edges of length 4 centimeters, what is the surface distance, in centimeters, between the lower left vertex on its front face and the upper right vertex on its back face?

(A) 8

(B) 4 √5

(D) 12√2

(E) 4√2+4

解：

请注意，surface距离，并非直线距离，可以想象将两个正方形平面展开。相当于是一个长方形的对角线的距离。答案为根号80，即，4 √5，答案为B。

31.

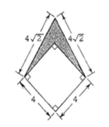
In the figure above, the area of the shaded region is

(A) 8√2

(B) 4√3

(D) 8(√3-1)

(E) 8(√2-1)

解：

本题需要做一个辅助线，连接正方形的水平对角线。由勾股定理可得该对角线的长度为4√2。则带着阴影部分的三角形为等边三角形。阴影部分的面积等于该等边三角形的面积减去一半的正方形面积，答案为D。

32.

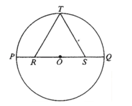
In the figure above, PQ is a diameter of circle O, PR=SQ, and △RST is equilateral. If the length of PQ is 2, what is the length of RT?

(A) 1/2

(B) 1/√3

(D) 2/√3

(E) √3

解：

三角形RTS是等边三角形，R是60度。由于PR=SQ，所以RO = OS，连接TO，基于等腰三角形的三线合一属性可知，TO垂直于RS。由于TO是半径，所以TO = 1。根据60度的cos可知，RT = 2/√3，答案为D。

33.A circular rim 28 inches in diameter rotates the same number of inches per second as a circular rim 35 inches in diameter. If the smaller rim makes x revolutions per second, how many revolutions per minute does the larger rim make in terms of x?

(A) 48π/x

(B) 75x

(D) 24x

(E) x/75

解：

题干的意思：小圈直径28，大圈直径35，这里是4：5。两个圈每秒转的周长一样。设大圈每秒转动的圈数为y

2π*14*x=2π*17.5*y

题目求1 min

则60y=（4X/5）*60=48X，答案为C。

34. Rita and Sam play the following game with n sticks on a table. Each must remove 1, 2, 3, 4 or 5 sticks at a time on alternate tums, and no stick that is removed is put back on the table. The one who removes the last stick(or sticks) from the table wins. If Rita goes first, which of the following is a value of n such that Sam can always win no matter how Rita plays？

(A) 7

(B) 10

(D) 12

(E) 16

解：

无论Rita先拿走几根木棍，Sam总能够使第一个来回两人拿走的木棍总数为6，举个例子，如果Rita先拿走1个，Sam就拿走5个，如果Rita拿走5个，Sam就拿走1个。所以，选项中是6的倍数的是正确选项，无论Rita怎么拿，Sam都会赢，答案为D。

35. Ben and Ann are among 7 contestants from which 4 semifinalists are to be selected. Of the different possible selections, how many contain neither Ben nor Ann?

(A) 5

(B) 6

(D) 14

(E) 21

解：

题目要求既不含Ben又不含Ann，剩下的5个里面挑4个，故选A。

36.

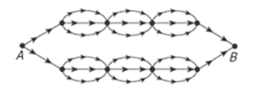
The map above shows the trails through a wilderness area. If travel is in the direction of the arrows, how many routes along the marked trails are possible from point A to point B?

(A) 11

(B) 18

(D) 108

(E) 432

解：

本题的图，基本是排列组合中的乘法原理图。

上面：3*3*3=27

下面：3*3*3=27

27+27=54，答案为C。

37.

Pat will walk from intersection X to intersection Y along a route that is confined to the square grid of four streets and three avenues shown in the map above. How many routes from X to Y can Pat take that have the minimum possible length?

(A) Six

(B) Eight

(D) Fourteen

(E) Sixteen

解：

本题很有难度，需要先理解Pat行走的本质。如果想从X走到Y，最少一定要横着走两格，竖着走三格，题目无非是问我们Pat到底什么时候需要横着走，什么时候需要竖着走。我们假设横着走一格是a，竖着走一格是b，这个问题就简化成了aabbb这五个字母的排列问题。例如aabbb就是先横着走两格，再竖着走三格，bbbaa就是先竖着走三格，再横着走两格。aabbb的排列方式为五个不同字母的全排列除以两个a以及三个b的顺序，答案为10。

38. If s/t =2, then the value of which of the following can be determined?

I 2t/s

II (s−t)/t

III (t−1)/(s−1)

(A) I only

(B) III only

(D) II and III only

(E) I and II and III

解：

依题意可知，s = 2t。可以发现，I和II均可以将t约掉，只有III中的t无法约掉，答案为C。

39. If 2x+5y=8 and 3x=2y, what is the value of 2x+y?

(A) 4

(B) 70/19

(D) 56/19

(E) 40/19

解：

本题十分简单。由题意可知，y = (3/2)x，带入2x+5y=8，可得，2x + (15/2)x = 8，x = 16/19。问题问的是(7/2)x的值。(7/2)*(16/19) = 56/19，答案为D。

40. When 2/9 of the votes on a certain resolution have been counted, 3/4 of those counted are in favor of the resolution. What fraction of the remaining votes must be against the resolution so that the total count will result in a vote of 2 to 1 against the resolution?

(A) 11/14

(B) 13/18

(D) 3/7

(E) 3/14

解：

先把题目看懂。题意为：在2/9counted的人中，有1/4投了反对票，3/4投了赞成票。题目问在剩余的7/9uncounted的票中，有多少投了反对票才能使得总的票数有2/3的反对票？答案为：2/9*1/4+7/9*x=2/3。解得x = 11/14，答案为A。

41.The sum of the first 100 positive integers is 5,050. What is the sum of the first 200 positive integers?

(A) 10,100

(B) 10,200

(D) 20,050

(E) 20,100

解：

101到200的和相当于1到100的和后面每个数都加上100，5050*2 + 100*100 = 20100，答案为E。