题库 / GMATAdvanced-PS-14
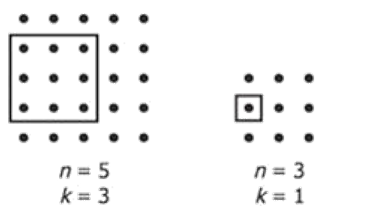
Let n and k be positive integers with k ≤ n. From an n × n array of dots, a k × k array of dots is selected.The figure above shows two examples where the selected k × k array is enclosed in a square. How many pairs (n, k) are possible so that exactly 48 of the dots in the n × n array are NOT in the selected k × k array?
1
2
3
4
5
还没有题目讲解(毕出老师会陆续发布对官方考题的解读,请保持关注)。
(n - k) * (n + k) = 48
计算48可以分解成多少个2数相乘的组合,48 因数分解:(2,2,2,2,3),可以分解成多少个两数相乘
(2,24), (4,12), (8,6), (16,3)
小的数=n-k,大的数=n+k,因为n-k+n+k=2n,n是整数,所以两数的和只能是偶数,去掉(16,3) 的组合,剩下3组。
【引用】考的是因式分解+因子分解+奇偶性
求不在范围内的点=n^2-k^2=(n+k)*(n-k)
(n - k) * (n + k) = 48
计算48可以分解成多少个2数相乘的组合,48 因数分解:(2,2,2,2,3),可以分解成多少个两数相乘
(2,24), (4,12), (8,6), (16,3)
小的数=n-k,大的数=n+k,因为n-k+n+k=2n,n是整数,所以两数的和只能是偶数,去掉(16,3) 的组合,剩下3组。
(n+k)(n-k)=48
可能的情况有1*48 2*24 3*16 4*12 6*8
因为n+k+n-k=2n是个偶数 所以1*48和3*16被排除 剩下3租
怎么题目都虚化了呢
+1 我以为我的出问题了
已经解决了哦,方法一:只需在【题库】https://bichu.com.cn/question 搜索"芝麻开门"即可移除雾化效果。
方法二:Chrome浏览器可安装热心网友提供的破解插件https://chrome.google.com/webstore/detail/edmedpcljopnjmddaaigmciiagcghndp
完成后自动显示完整考题
厉害了,谢谢分享。 为中国人的智慧点赞
登录 或 注册 后可以参加讨论
n2-k2=48 -> (n+k)(n-k)=48 ->(2x+y)y=48,y比为偶数->48分解偶数组合为2x24,4x12,8x6三组
真尼玛不应该,最后竟然数漏了一个K=1.。。。。。!!!!!
再停下来多想两秒钟。。。。。n*n - k*k = 48
(n - k) * (n + k) = 48
n = 7, k = 1
n = 13, k = 11
n = 8, k = 4
n*n - k*k = 48
(n - k) * (n + k) = 48
n = 7, k = 1
n = 13, k = 11
n = 8, k = 4
b