题库 / GMATAdvanced-PS-5
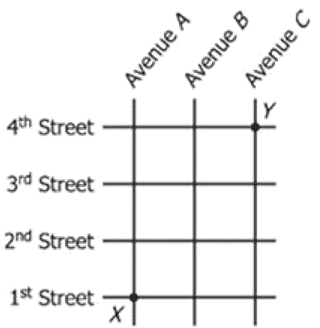
Pat will walk from intersection X to intersection Y along a route that is confined to the square grid of four streets and three avenues shown in the map above. How many routes from X to Y can Pat take that have the minimum possible length?
Six
Eight
Ten
Fourteen
Sixteen
还没有题目讲解(毕出老师会陆续发布对官方考题的解读,请保持关注)。
网格路径问题
无论路径如何,从X到Y都需要经过3条street和2条avenue,相当于从5个里面挑3个street,street确定了,avenue自然就确定了。
请问为什么相对于是在5个里挑3个呢~这类问题还是不太理解~
最短路径X→Y,无论哪种走法,必须经过3竖2横,即3次向上和2次向右。就是你从一个点出发,要走5步,其中3步向上,2步向右,都能到达同一个点,问有多少种不同的走法。
再直白来说,相当于你有3个一样的苹果,2个一样的梨,将它们排成一排,有多少种排法。
希望能够帮助到你
谢谢~确实是这个思路。
登录 或 注册 后可以参加讨论
C(5,3)=10
一共是五步,必须是三步向上,两步向右,至于怎么分配,随机, c 52 或者c53 。
右2步,上3步。堪称5个要素的排列组合,就是5!/(2!*3!)
同类题型同理
理解:一共五个坑位,随机选择两个来放向右走,那就是C52五个里面随机选2
就相当于是用五根木棍(两横三竖的)排列组合:|-|-|
必须走5步,且3个向上2个向右。5步选3步向上 or 5步选2步向右。
好的!谢谢!