题库 / GMATAdvanced-PS-7
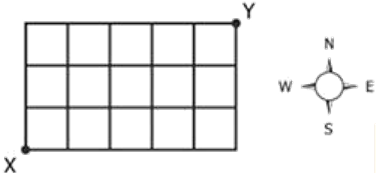
In the figure above, X and Y represent locations in a district of a certain city where the streets form a rectangular grid.In traveling only north or east along the streets from X to Y, how many different paths are possible?
720
512
336
256
56
还没有题目讲解(毕出老师会陆续发布对官方考题的解读,请保持关注)。
网格路径问题
从X到Y必须经过5横3竖,相当于8个里面选5个,横向路径确定,竖向自然就确定了,C85=56
这题目的是走最短的8步到终点。最重要的是要意识到如果横固定了,竖自然就固定了;如果竖固定了,横也自然固定了。那么就是三个竖有八种选择(可以选择在第一步,第二步。。。第八步走竖),或者5个横有8种选择。剩下的就相当于把三个棍丢到8个坑里怎么丢了。自然就是c(8,3)了。。。
C(8,3)
从X走到Y一定要走五个横线和三个竖线,A1~A5是横线,B1~B3是竖线,那就一共有8!种组合,又因为A都是一样的,B都是一样的,需要排除重复的组合,所以是8!/(5!3!)=56
不理解为什么是这样。。。。硬记下来这个最短路径就是A(8,8)/[A(5,5)A(3,3)]=56
网格路径问题
从X到Y必须经过5横3竖,相当于8个里面选5个,横向路径确定,竖向自然就确定了,C85=56
好多解析都是你,感谢🙏
哈哈其实也没什么啦,这也是为了在杀G路上督促自己,祝早日分手
赞
登录 或 注册 后可以参加讨论