GMAT考题：OG2017Q-DS-208

GMAT考题

题库 / OG2017Q-DS-208

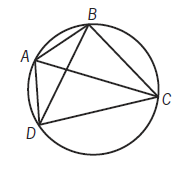
In the figure shown, quadrilateral ABCD is inscribed in a circle of radius 5. What is the perimeter of quadrilateral ABCD ?

(1) The length of AB is 6 and the length of CD is 8.

(2) AC is a diameter of the circle.

Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.

Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.

BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.

EACH statement ALONE is sufficient.

Statements (1) and (2) TOGETHER are NOT sufficient.

考题讲解

毕出

题目分析：

（1）仅有条件1中的AB和CD长，无法求得AD和BC长，也就无法求得四边形ABCD的周长。

（2） AC是直径，所以有AC=2*5=10，仅有AC长也无法计算周长。

结合条件1和条件2，由定理“直径所对的圆周角为直角”可知，角ABC和角ADC均为直角，由勾股定理得~$AD=\sqrt{AC^2-CD^2}$~，即~$AD=\sqrt{10^2-8^2}$~=4，~$BC=\sqrt{AC^2-AB^2}$~，即~$BC=\sqrt{10^2-6^2}=8$~，所以四边形ABCD的周长为AB+BC+CD+AD=6+8+4+8=26。

因此，本题答案为（C），两个条件结合起来才能解题，任何单独一个均不行。

展开显示