题库 / OG2017Q-DS-299
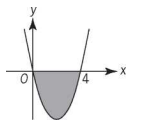
In the xy-plane shown, the shaded region consists of all points that lie above the graph of~$ y = x^2 - 4x$~ and below the x-axis. Does the point (a,b) (not shown) lie in the shaded region if b < 0 ?
(1) 0 < a < 4
(2) ~$ a^2 - 4a < b$~
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
题目分析:
由于曲线解析式为~$y=x^2-4x$~,所以令y=0,解得曲线与x轴交点为(0,0)和(4,0)。本题判断(a,b)是否位于阴影区域。在阴影区域(曲线上方)的点(a,b)满足~$a^2-4a<b$~
(1) 0<a<4,同时b<0,由于不知道b的范围,所以无法判断。例如a=2,b=-1符合要求,(2,1)点在阴影区域内。又如a=2,b=-10符合要求,(2,-10)点不在阴影区域内,所以,条件1无法判断点(a,b)是否位于阴影区域内,不满足要求。
(2) 满足条件2的点一定位于阴影区域内。
因此,本题答案为(B),仅条件2可以解题,条件1不行
(2) 满足条件2的点一定位于阴影区域内。 ---条件2 就是抛物线的式子。
登录 或 注册 后可以参加讨论