扫描二维码，直接登录
题库 / OG2017Q-PS-134
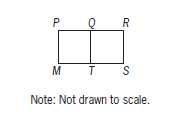
In the figure shown above, line segment QR has length 12, and rectangle MPQT is a square. If the area of rectangular region MPRS is 540, what is the area of rectangular region TQRS ?
144
216
324
360
396
MPQT是正方形，假设边长a，则说MPQT的面积是a^2。
QT是MPQT和QTSR的共同边，因此QTSR的面积是a*12。
这两个四边形的面积加和等于整个大长方形PMRS的面积，即，a^2+12*a=540
可以求得a=18
所以TQRS的面积为18*12=216，答案为B。
MPQT是正方形，假设边长a,所以说Smpot=a^2
QT是MPQT和QTSR的共同边，a
Sqtsr=12*a
Spmtq+Sqtsr=a^2+12*a=540
可以求得x=18
所以Sqtsr=18*12=216
没图！
求图