扫描二维码，直接登录
题库 / GMATAdvanced-PS-14
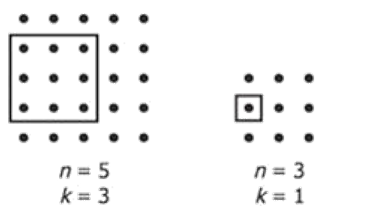
Let n and k be positive integers with k ≤ n. From an n × n array of dots, a k × k array of dots is selected.The figure above shows two examples where the selected k × k array is enclosed in a square. How many pairs (n, k) are possible so that exactly 48 of the dots in the n × n array are NOT in the selected k × k array?
1
2
3
4
5
还没有题目讲解（毕出老师会陆续发布对官方考题的解读，请保持关注）。
【引用】考的是因式分解+因子分解+奇偶性
求不在范围内的点=n^2-k^2=(n+k)*(n-k)
(n - k) * (n + k) = 48
计算48可以分解成多少个2数相乘的组合，48 因数分解：(2,2,2,2,3),可以分解成多少个两数相乘
(2，24), (4，12), (8，6), (16，3)
小的数=n-k，大的数=n+k，因为n-k+n+k=2n,n是整数，所以两数的和只能是偶数,去掉(16，3) 的组合，剩下3组。
登录 或 注册 后可以参加讨论