题库 / GMATLA-PS-41
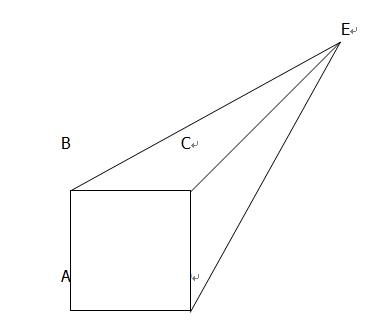
In the figure, each side of square ABCD has length 1, the length of line segment CE is 1, and the length of line segment BE is equal to the length of line segment DE. What is the area of the triangular region BCE?
~$\frac{1}{3}$~
~$\frac{\sqrt{2}}{4}$~
~$\frac{1}{2}$~
~$\frac{\sqrt{2}}{2}$~
~$\frac{3}{4}$~
还没有题目讲解(毕出老师会陆续发布对官方考题的解读,请保持关注)。
这居然是个平面几何。。。这也太坑了。。。
“连接正方形对角线,交点为o。BCE的面积=BOE的面积-BOC的面积”
这道题的解题关键是不要被图片误导。这是一道平面几何题,不是立体几何。而且根据题目给出的信息,斜线CE和正方形四条边应该是等长的,图中的线长短明显不一样,存在误导效果。
知道了这些信息,之后的解题就比较简单了。图中说,BE=DE 所以直观的看,CE就是“斜着出去的”,就是说,正方形的对角线AC和CE是一条直线上。而我们又知道正方形里面对角线AC和BD是相互垂直的。
因此三角形BCE的面积,等于底乘高的一半,底就是CE, 高就是BD的一半,就是sqrt(2)/2 二分之根号二。所以面积就是sqrt(2)/2*1的一半 = B答案。。
居然不是立体几何加一
可以用正弦定理去做,1/2absina=S
利用了等腰三角形底边高与底边中分线是同一条线的性质,证明了BCE的高其实就是正方形对角线的一半
算不出来的是时候作辅助线看看能不能通过其他图形减出来
看成立体+1,算了好久没算出来,平面的话做调辅助线底乘以高就可以算出来了
先观察啊宝贝,先观察,低跟高识别出来就比较好算了。
哪能看出不是立体几何?
用时太长了!考试估计要直接跳过了。图太有误导性。利用了等腰三角形底边高与底边中分线是同一条线的性质,所以AC和CE在一条线上。BD垂直AC,所以直接底乘高除2 可得
从已知条件中可以得出area of BCE 肯定小于 1/2. 所以只能从 A 或 B 中选。B 比 A 看着更靠谱些。:)
这题耗时有点久了,延展BC, 并让E做垂线与BC延长线垂直相交,即可得到一个等腰直角三角形。然后利用斜边算边长,然后计算体积
我佛了。
绝了,不是立体几何
这是一道平面几何题,不是立体几何。这是一道平面几何题,不是立体几何。这是一道平面几何题,不是立体几何。
连接正方形对角线,交点为o。BCE的面积=BOE的面积-BOC的面积
这图画的 直接就觉得是立体图
不是立体图形,是平面图形,注意!!
1 这是一个平面图形 2 CE可以看作是AC的延伸线 3 把AC的一半看作延伸线,BD的一半则是三角形BCE的外高
直接脑补成锥形做了...